Paths

题意翻译

给定一张 $n$ 个顶点的图，对于点 $i,j$，如果 $\gcd(i,j)\neq 1$，则 $i$ 到 $j$ 有一条长度为 $1$ 的无向边。令 $dis(i,j)$ 表示从 $i$ 到 $j$ 的最短路，如果 $i$ 无法到 $j$，则 $dis(i,j)=0$。求节点两两之间距离之和。 $n \leq 10^7$。

题目描述

You are given a positive integer $ n $ . Let's build a graph on vertices $ 1,2,...,n $ in such a way that there is an edge between vertices $ u $ and $ v $ if and only if 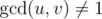. Let $ d(u,v) $ be the shortest distance between $ u $ and $ v $ , or $ 0 $ if there is no path between them. Compute the sum of values $ d(u,v) $ over all $ 1<=u<v<=n $ . The $ gcd $ (greatest common divisor) of two positive integers is the maximum positive integer that divides both of the integers.

输入输出格式

输入格式

Single integer $ n $ ( $ 1<=n<=10^{7} $ ).

输出格式

Print the sum of $ d(u,v) $ over all $ 1<=u<v<=n $ .

输入输出样例

输入样例 #1

6

输出样例 #1

8

输入样例 #2

10

输出样例 #2

44

说明

All shortest paths in the first example: -  -  -  -  -  -  There are no paths between other pairs of vertices. The total distance is $ 2+1+1+2+1+1=8 $ .

题意翻译

给定一张 $n$ 个顶点的图，对于点 $i,j$，如果 $\gcd(i,j)\neq 1$，则 $i$ 到 $j$ 有一条长度为 $1$ 的无向边。令 $dis(i,j)$ 表示从 $i$ 到 $j$ 的最短路，如果 $i$ 无法到 $j$，则 $dis(i,j)=0$。求节点两两之间距离之和。 $n \leq 10^7$。