Mister B and Angle in Polygon

题意翻译

### 题目描述 在一个边为 $n$ 的正凸多边形上，有一个角 $a$。 现在要找到三个不同的顶点 $v1$ , $v2$ , $v3$ 使得 $∠ v1 v2 v3$ （其中 $v2$ 是角度的顶点，并且 $v1$ 和 $v3$ 位于其两侧）尽可能接近 $a$（换句话说，该值应该尽可能小）。 如果有多个最优解，可以输出**任意一个**。 ### 输入格式 一行包含两个空格分隔的整数 $n$ 和 $a$ ( $3<=n<=10^{5}$ , $1<=a<=180$) $n$ 表示多边形中的顶点数，$a$表示所需的角度，以度为单位。 ### 输出格式 输出三个空格分隔的整数：$∠ v1 v2 v3$ 的顶点 $v1$ , $v2$ , $v3$ 。如果有多个最优解，输出其中**任意一个**。 顶点按**顺时针**顺序从 $1$ 到 $n$ 编号。

题目描述

On one quiet day all of sudden Mister B decided to draw angle $ a $ on his field. Aliens have already visited his field and left many different geometric figures on it. One of the figures is regular convex $ n $ -gon (regular convex polygon with $ n $ sides). That's why Mister B decided to use this polygon. Now Mister B must find three distinct vertices $ v_{1} $ , $ v_{2} $ , $ v_{3} $ such that the angle  (where $ v_{2} $ is the vertex of the angle, and $ v_{1} $ and $ v_{3} $ lie on its sides) is as close as possible to $ a $ . In other words, the value 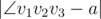 should be minimum possible. If there are many optimal solutions, Mister B should be satisfied with any of them.

输入输出格式

输入格式

First and only line contains two space-separated integers $ n $ and $ a $ ( $ 3<=n<=10^{5} $ , $ 1<=a<=180 $ ) — the number of vertices in the polygon and the needed angle, in degrees.

输出格式

Print three space-separated integers: the vertices $ v_{1} $ , $ v_{2} $ , $ v_{3} $ , which form . If there are multiple optimal solutions, print any of them. The vertices are numbered from $ 1 $ to $ n $ in clockwise order.

输入输出样例

输入样例 #1

3 15

输出样例 #1

1 2 3

输入样例 #2

4 67

输出样例 #2

2 1 3

输入样例 #3

4 68

输出样例 #3

4 1 2

说明

In first sample test vertices of regular triangle can create only angle of $ 60 $ degrees, that's why every possible angle is correct. Vertices of square can create $ 45 $ or $ 90 $ degrees angles only. That's why in second sample test the angle of $ 45 $ degrees was chosen, since $ |45-67|&lt;|90-67| $ . Other correct answers are: "3 1 2", "3 2 4", "4 2 3", "4 3 1", "1 3 4", "1 4 2", "2 4 1", "4 1 3", "3 1 4", "3 4 2", "2 4 3", "2 3 1", "1 3 2", "1 2 4", "4 2 1". In third sample test, on the contrary, the angle of $ 90 $ degrees was chosen, since $ |90-68|&lt;|45-68| $ . Other correct answers are: "2 1 4", "3 2 1", "1 2 3", "4 3 2", "2 3 4", "1 4 3", "3 4 1".