Fake bullions

题意翻译

给定一张 $n$ 个点的竞赛图,第 $i$ 个点上有 $S_i$ 个人,编号从 $0$ 到 $S_i-1$，其中的某一些人手上有真金条。 在时刻 $T$，如果从 $u$ 到 $v$ 有一条边,并且 $u$ 中第 $T\bmod S_u$ 个人手上有金条(无论真假),并且 $v$ 中第 $T \bmod S_v$ 个人没有金条,那么 $v$ 中第 $T \bmod S_v$ 个人会获得一个假金条. 当所有人手上的金条数目不再变化时,他们开始卖出金条,真金条一定会卖出去,而假金条可能卖出去也可能卖不出去. 现在从卖出金条最多的 $A$ 个点中随机选择 $B$ 个，问可能选出的城市集合有多少个。

题目描述

In Isart people don't die. There are $ n $ gangs of criminals. The $ i $ -th gang contains $ s_{i} $ evil people numerated from $ 0 $ to $ s_{i}-1 $ . Some of these people took part in a big mine robbery and picked one gold bullion each (these people are given in the input). That happened $ 10^{100} $ years ago and then all of the gangs escaped to a remote area, far from towns. During the years, they were copying some gold bullions according to an organized plan in order to not get arrested. They constructed a tournament directed graph (a graph where there is exactly one directed edge between every pair of vertices) of gangs (the graph is given in the input). In this graph an edge from $ u $ to $ v $ means that in the $ i $ -th hour the person 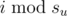 of the gang $ u $ can send a fake gold bullion to person 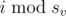 of gang $ v $ . He sends it if he has some bullion (real or fake), while the receiver doesn't have any. Thus, at any moment each of the gangsters has zero or one gold bullion. Some of them have real bullions, and some of them have fake ones. In the beginning of this year, the police has finally found the gangs, but they couldn't catch them, as usual. The police decided to open a jewelry store so that the gangsters would sell the bullions. Thus, every gangster that has a bullion (fake or real) will try to sell it. If he has a real gold bullion, he sells it without problems, but if he has a fake one, there is a choice of two events that can happen: - The person sells the gold bullion successfully. - The person is arrested by police. The power of a gang is the number of people in it that successfully sold their bullion. After all selling is done, the police arrests $ b $ gangs out of top gangs. Sort the gangs by powers, we call the first $ a $ gang top gangs(you can sort the equal powers in each order). Consider all possible results of selling fake gold bullions and all possible choice of $ b $ gangs among the top gangs. Count the number of different sets of these $ b $ gangs modulo $ 10^{9}+7 $ . Two sets $ X $ and $ Y $ are considered different if some gang is in $ X $ and isn't in $ Y $ .

输入输出格式

输入格式

The first line contains four integers $ n $ , $ a $ and $ b $ ( $ 1<=b<=a<=n<=5·10^{3} $ ) — the number of gangs, the constants $ a $ and $ b $ from the statement. Then $ n $ lines follow, each line contains a string of size $ n $ consisting of zeros and ones. The $ j $ -th character in the $ i $ -th of these lines is equal to $ 1 $ , then the vertex $ i $ have a directed edge to the vertex $ j $ . It is guaranteed that $ a_{ii}=0 $ and $ a_{ij}+a_{ji}=1 $ if $ i≠j $ . Then $ n $ lines follow, each line starts with the integer $ s_{i} $ ( $ 1<=s_{i}<=2·10^{6} $ ) — the number of gangsters in the $ i $ -th gang, and then contains a string of zeros and ones with length $ s_{i} $ . The $ j $ -th character is $ 0 $ if the $ j $ -th person of the $ i $ -th gang had a real gold bullion initially, otherwise it is $ 1 $ . It is guaranteed that the sum of $ s_{i} $ does not exceed $ 2·10^{6} $ .

输出格式

Print single integer: the number of different sets of $ b $ gangs the police can arrest modulo $ 10^{9}+7 $ .

输入输出样例

输入样例 #1

2 2 1
01
00
5 11000
6 100000

输出样例 #1

2

输入样例 #2

5 2 1
00000
10000
11011
11000
11010
2 00
1 1
6 100110
1 0
1 0

输出样例 #2

5