Volatile Kite

题意翻译

按顺时针顺序给你平面上的 $n$ 个点，保证这 $n$ 个点能够构成一个凸多边形。 要求你求出一个最大的 $d$，使得这 $n$ 个点在离原来位置不超过 $d$ 的范围内任意移动，都能够保证这 $n$ 个点构成的多边形是凸的且不会自交。 其中 $4\le n\le 1\times 10^3$，$-10^9\le x_i,y_i\le 10^9$。

题目描述

You are given a convex polygon $ P $ with $ n $ distinct vertices $ p_{1},p_{2},...,p_{n} $ . Vertex $ p_{i} $ has coordinates $ (x_{i},y_{i}) $ in the 2D plane. These vertices are listed in clockwise order. You can choose a real number $ D $ and move each vertex of the polygon a distance of at most $ D $ from their original positions. Find the maximum value of $ D $ such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.

输入输出格式

输入格式

The first line has one integer $ n $ ( $ 4<=n<=1000 $ ) — the number of vertices. The next $ n $ lines contain the coordinates of the vertices. Line $ i $ contains two integers $ x_{i} $ and $ y_{i} $ ( $ -10^{9}<=x_{i},y_{i}<=10^{9} $ ) — the coordinates of the $ i $ -th vertex. These points are guaranteed to be given in clockwise order, and will form a strictly convex polygon (in particular, no three consecutive points lie on the same straight line).

输出格式

Print one real number $ D $ , which is the maximum real number such that no matter how you move the vertices, the polygon stays convex. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ . Namely, let's assume that your answer is $ a $ and the answer of the jury is $ b $ . The checker program will consider your answer correct if .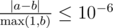

输入输出样例

输入样例 #1

4
0 0
0 1
1 1
1 0

输出样例 #1

0.3535533906

输入样例 #2

6
5 0
10 0
12 -4
10 -8
5 -8
3 -4

输出样例 #2

1.0000000000

说明

Here is a picture of the first sample  Here is an example of making the polygon non-convex.  This is not an optimal solution, since the maximum distance we moved one point is $ ≈0.4242640687 $ , whereas we can make it non-convex by only moving each point a distance of at most $ ≈0.3535533906 $ .