Bear and Colors

题意翻译

Limak 有 $n$ 个球，从左到右编号依次为 $1 \dots n$。同时又有 $n$ 种颜色，从编号依次为 $1 \dots n$。第 $i$ 个球的编号为 $t_i$。 对于球中每一个固定的段（含有连续元素的集合），可以定义一个**主要颜色**，即此段中出现次数最多的颜色。在可以有多种主要颜色的情况下，选择编号最小的。 现有 $\dfrac{n(n + 1)}{2}$ 个不为空的段。对于每个颜色，你需要输出此颜色作为主要颜色的次数。

题目描述

Bear Limak has $ n $ colored balls, arranged in one long row. Balls are numbered $ 1 $ through $ n $ , from left to right. There are $ n $ possible colors, also numbered $ 1 $ through $ n $ . The $ i $ -th ball has color $ t_{i} $ . For a fixed interval (set of consecutive elements) of balls we can define a dominant color. It's a color occurring the biggest number of times in the interval. In case of a tie between some colors, the one with the smallest number (index) is chosen as dominant. There are 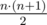 non-empty intervals in total. For each color, your task is to count the number of intervals in which this color is dominant.

输入输出格式

输入格式

The first line of the input contains a single integer $ n $ ( $ 1<=n<=5000 $ ) — the number of balls. The second line contains $ n $ integers $ t_{1},t_{2},...,t_{n} $ ( $ 1<=t_{i}<=n $ ) where $ t_{i} $ is the color of the $ i $ -th ball.

输出格式

Print $ n $ integers. The $ i $ -th of them should be equal to the number of intervals where $ i $ is a dominant color.

输入输出样例

输入样例 #1

4
1 2 1 2

输出样例 #1

7 3 0 0 

输入样例 #2

3
1 1 1

输出样例 #2

6 0 0 

说明

In the first sample, color $ 2 $ is dominant in three intervals: - An interval $ [2,2] $ contains one ball. This ball's color is $ 2 $ so it's clearly a dominant color. - An interval $ [4,4] $ contains one ball, with color $ 2 $ again. - An interval $ [2,4] $ contains two balls of color $ 2 $ and one ball of color $ 1 $ . There are $ 7 $ more intervals and color $ 1 $ is dominant in all of them.