Bear and Polynomials

题意翻译

定义一个合法多项式满足以下条件 - 每一个系数都是整数 - 每一个系数的绝对值 $\le k$，其中 $k$ 是一个给定的整数 - 最高次项系数 $\neq0$ 给你一个 $n$ 次多项式 $P(x)=\sum\limits_{i=0}^{n} a_i\cdot x_i$ 保证 $P(2)\neq0$ 现在给你一个机会，可以随意改变一个系数，使得原多项式变成 $Q(x)$ 要满足 $Q(x)$ 合法 问你有多少种不同 $Q(x)$ $n$ 次多项式不同定义为 $\exists x,0\le x\le n,a_x\neq a'_{x}$

题目描述

Limak is a little polar bear. He doesn't have many toys and thus he often plays with polynomials. He considers a polynomial valid if its degree is $ n $ and its coefficients are integers not exceeding $ k $ by the absolute value. More formally: Let $ a_{0},a_{1},...,a_{n} $ denote the coefficients, so 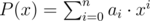. Then, a polynomial $ P(x) $ is valid if all the following conditions are satisfied: - $ a_{i} $ is integer for every $ i $ ; - $ |a_{i}|<=k $ for every $ i $ ; - $ a_{n}≠0 $ . Limak has recently got a valid polynomial $ P $ with coefficients $ a_{0},a_{1},a_{2},...,a_{n} $ . He noticed that $ P(2)≠0 $ and he wants to change it. He is going to change one coefficient to get a valid polynomial $ Q $ of degree $ n $ that $ Q(2)=0 $ . Count the number of ways to do so. You should count two ways as a distinct if coefficients of target polynoms differ.

输入输出格式

输入格式

The first line contains two integers $ n $ and $ k $ ( $ 1<=n<=200000,1<=k<=10^{9} $ ) — the degree of the polynomial and the limit for absolute values of coefficients. The second line contains $ n+1 $ integers $ a_{0},a_{1},...,a_{n} $ ( $ |a_{i}|<=k,a_{n}≠0 $ ) — describing a valid polynomial 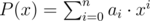. It's guaranteed that $ P(2)≠0 $ .

输出格式

Print the number of ways to change one coefficient to get a valid polynomial $ Q $ that $ Q(2)=0 $ .

输入输出样例

输入样例 #1

3 1000000000
10 -9 -3 5

输出样例 #1

3

输入样例 #2

3 12
10 -9 -3 5

输出样例 #2

2

输入样例 #3

2 20
14 -7 19

输出样例 #3

0

说明

In the first sample, we are given a polynomial $ P(x)=10-9x-3x^{2}+5x^{3} $ . Limak can change one coefficient in three ways: 1. He can set $ a_{0}=-10 $ . Then he would get $ Q(x)=-10-9x-3x^{2}+5x^{3} $ and indeed $ Q(2)=-10-18-12+40=0 $ . 2. Or he can set $ a_{2}=-8 $ . Then $ Q(x)=10-9x-8x^{2}+5x^{3} $ and indeed $ Q(2)=10-18-32+40=0 $ . 3. Or he can set $ a_{1}=-19 $ . Then $ Q(x)=10-19x-3x^{2}+5x^{3} $ and indeed $ Q(2)=10-38-12+40=0 $ . In the second sample, we are given the same polynomial. This time though, $ k $ is equal to $ 12 $ instead of $ 10^{9} $ . Two first of ways listed above are still valid but in the third way we would get $ |a_{1}|&gt;k $ what is not allowed. Thus, the answer is $ 2 $ this time.