Startup Funding

题意翻译

题目有一点点复杂。  有n（1 <= n <=10^6）周，第A周有V[A]和C[A]两个值，题目定义了区间[L,R]对应的值的计算p(L,R)=min(100*max(区间内的V),min(区间内的C))。 现在，对于每个L值，都有一个可以最大化p(L,R)值的R，假设当左端点为L时，最大的p(L,R)的值为Q[L]。 题目问，在这些L值中，随机选择k个作为L值，对于每个L值计算可能达到的最大p(L,R)，然后求平均数，问这个结果的数学期望是多少。

题目描述

An e-commerce startup pitches to the investors to get funding. They have been functional for $ n $ weeks now and also have a website! For each week they know the number of unique visitors during this week $ v_{i} $ and the revenue $ c_{i} $ . To evaluate the potential of the startup at some range of weeks from $ l $ to $ r $ inclusive investors use the minimum among the maximum number of visitors multiplied by $ 100 $ and the minimum revenue during this period, that is: 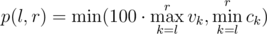The truth is that investors have no idea how to efficiently evaluate the startup, so they are going to pick some $ k $ random distinct weeks $ l_{i} $ and give them to managers of the startup. For each $ l_{i} $ they should pick some $ r_{i}>=l_{i} $ and report maximum number of visitors and minimum revenue during this period. Then, investors will calculate the potential of the startup for each of these ranges and take minimum value of $ p(l_{i},r_{i}) $ as the total evaluation grade of the startup. Assuming that managers of the startup always report the optimal values of $ r_{i} $ for some particular $ l_{i} $ , i.e., the value such that the resulting grade of the startup is maximized, what is the expected resulting grade of the startup?

输入输出格式

输入格式

The first line of the input contains two integers $ n $ and $ k $ ( $ 1<=k<=n<=1000000 $ ). The second line contains $ n $ integers $ v_{i} $ ( $ 1<=v_{i}<=10^{7} $ ) — the number of unique visitors during each week. The third line contains $ n $ integers $ c_{i} $ ( $ 1<=c_{i}<=10^{7} $ ) —the revenue for each week.

输出格式

Print a single real value — the expected grade of the startup. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ . Namely: let's assume that your answer is $ a $ , and the answer of the jury is $ b $ . The checker program will consider your answer correct, if .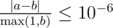

输入输出样例

输入样例 #1

3 2
3 2 1
300 200 300

输出样例 #1

133.3333333

说明

Consider the first sample. If the investors ask for $ l_{i}=1 $ onwards, startup will choose $ r_{i}=1 $ , such that max number of visitors is $ 3 $ and minimum revenue is $ 300 $ . Thus, potential in this case is $ min(3·100,300)=300 $ . If the investors ask for $ l_{i}=2 $ onwards, startup will choose $ r_{i}=3 $ , such that max number of visitors is $ 2 $ and minimum revenue is $ 200 $ . Thus, potential in this case is $ min(2·100,200)=200 $ . If the investors ask for $ l_{i}=3 $ onwards, startup will choose $ r_{i}=3 $ , such that max number of visitors is $ 1 $ and minimum revenue is $ 300 $ . Thus, potential in this case is $ min(1·100,300)=100 $ . We have to choose a set of size $ 2 $ equi-probably and take minimum of each. The possible sets here are : $ {200,300} $ , $ {100,300} $ , $ {100,200} $ , effectively the set of possible values as perceived by investors equi-probably: $ {200,100,100} $ . Thus, the expected value is $ (100+200+100)/3=133.(3) $ .

题意翻译

题目有一点点复杂。  有n（1 <= n <=10^6）周，第A周有V[A]和C[A]两个值，题目定义了区间[L,R]对应的值的计算p(L,R)=min(100*max(区间内的V),min(区间内的C))。 现在，对于每个L值，都有一个可以最大化p(L,R)值的R，假设当左端点为L时，最大的p(L,R)的值为Q[L]。 题目问，在这些L值中，随机选择k个作为L值，对于每个L值计算可能达到的最大p(L,R)，然后求平均数，问这个结果的数学期望是多少。