Happy Tree Party

题意翻译

## 题目描述 为了庆祝博格丹的生日，他的母亲送给他一棵有$n$个节点的树，树的第$i$条边上写了一个数字$x_i$。顺带提醒一下，一棵树指的是一个由无向边连接的无环连通图。在礼物被送出之后，有$m$位访客陆续来到博格丹家中参加派对。第$i$位访客会进行如下两种操作其中之一： >1.选择一个数$y_i$和两个节点$a_i$、$b_i$。在这之后，他会沿着树的边走一遍从$a_i$到$b_i$的最短路（当然，在树上这样的路径只有一条）。每当他经过一条边$j$时，他选择的数$y_i$会立刻变成$\lfloor \frac{y_i}{x_j} \rfloor$，也就是$\frac{y_i}{x_i}$向下取整。 > >2.选择第$j$条边$p_j$，把它的边权$x_{p_i}$改成一个正整数$c_i \in [1,x_{p_i}]$。 由于博格丹很替他的客人们着想，他决定简化这个过程。你需要写一个程序处理访客们的操作，并且对于每一个第一种操作$i$，输出$y_i$最后的值。 ## 输入输出格式 ### 输入格式 输入的第一行包含两个整数$n$、$m$（$2\le n\le200000$，$1\le m\le200000$），分别表示树的节点数和访客的数量。 接下来$n-1$行描述每一条边的信息。这些行中的第$i$行包含三个整数$u_i$，$v_i$，$x_i$（$1\le u_i,v_i\le n,u_i\ne v_i,1\le x_i \le 10^{18}$），表示节点$u_i$和$v_i$之间有一条写有$x_i$的无向边。 接下来$m$行描述访客们的操作。每一行包含三个或者四个整数，有如下两种情况： * $1\ a_i\ b_i\ c_i\ $表示操作1 * $2\ p_i\ c_i\ $表示操作2 你可以认为每一个询问都是合法的，也就是说$1\le a_i,b_i\le n$，$1\le p_i\le n-1$，$1\le y_i\le10^{18}$并且$1\le c_i\le x_{p_i}$，此时的$x_{p_i}$不一定和最开始的$x_{p_i}$相等，因为它可能已经被更新过。所有边按照$1\sim n-1$的标号依次在输入中给出。 ### 输出格式 对于每一个询问1，输出一行，从$a_i$走到$b_i$后$y_i$最终的值

题目描述

Bogdan has a birthday today and mom gave him a tree consisting of $ n $ vertecies. For every edge of the tree $ i $ , some number $ x_{i} $ was written on it. In case you forget, a tree is a connected non-directed graph without cycles. After the present was granted, $ m $ guests consecutively come to Bogdan's party. When the $ i $ -th guest comes, he performs exactly one of the two possible operations: 1. Chooses some number $ y_{i} $ , and two vertecies $ a_{i} $ and $ b_{i} $ . After that, he moves along the edges of the tree from vertex $ a_{i} $ to vertex $ b_{i} $ using the shortest path (of course, such a path is unique in the tree). Every time he moves along some edge $ j $ , he replaces his current number $ y_{i} $ by 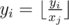, that is, by the result of integer division $ y_{i} $ div $ x_{j} $ . 2. Chooses some edge $ p_{i} $ and replaces the value written in it $ x_{pi} $ by some positive integer $ c_{i}<x_{pi} $ . As Bogdan cares about his guests, he decided to ease the process. Write a program that performs all the operations requested by guests and outputs the resulting value $ y_{i} $ for each $ i $ of the first type.

输入输出格式

输入格式

The first line of the input contains integers, $ n $ and $ m $ ( $ 2<=n<=200000 $ , $ 1<=m<=200000 $ ) — the number of vertecies in the tree granted to Bogdan by his mom and the number of guests that came to the party respectively. Next $ n-1 $ lines contain the description of the edges. The $ i $ -th of these lines contains three integers $ u_{i} $ , $ v_{i} $ and $ x_{i} $ ( $ 1<=u_{i},v_{i}<=n $ , $ u_{i}≠v_{i} $ , $ 1<=x_{i}<=10^{18} $ ), denoting an edge that connects vertecies $ u_{i} $ and $ v_{i} $ , with the number $ x_{i} $ initially written on it. The following $ m $ lines describe operations, requested by Bogdan's guests. Each description contains three or four integers and has one of the two possible forms: - $ 1 $ $ a_{i} $ $ b_{i} $ $ y_{i} $ corresponds to a guest, who chooses the operation of the first type. - $ 2 $ $ p_{i} $ $ c_{i} $ corresponds to a guests, who chooses the operation of the second type. It is guaranteed that all the queries are correct, namely $ 1<=a_{i},b_{i}<=n $ , $ 1<=p_{i}<=n-1 $ , $ 1<=y_{i}<=10^{18} $ and $ 1<=c_{i}&lt;x_{pi} $ , where $ x_{pi} $ represents a number written on edge $ p_{i} $ at this particular moment of time that is not necessarily equal to the initial value $ x_{pi} $ , as some decreases may have already been applied to it. The edges are numbered from $ 1 $ to $ n-1 $ in the order they appear in the input.

输出格式

For each guest who chooses the operation of the first type, print the result of processing the value $ y_{i} $ through the path from $ a_{i} $ to $ b_{i} $ .

输入输出样例

输入样例 #1

6 6
1 2 1
1 3 7
1 4 4
2 5 5
2 6 2
1 4 6 17
2 3 2
1 4 6 17
1 5 5 20
2 4 1
1 5 1 3

输出样例 #1

2
4
20
3

输入样例 #2

5 4
1 2 7
1 3 3
3 4 2
3 5 5
1 4 2 100
1 5 4 1
2 2 2
1 1 3 4

输出样例 #2

2
0
2

说明

Initially the tree looks like this: The response to the first query is:  = 2 After the third edge is changed, the tree looks like this: The response to the second query is:  = 4 In the third query the initial and final vertex coincide, that is, the answer will be the initial number 20. After the change in the fourth edge the tree looks like this: In the last query the answer will be:  = 3

题意翻译

## 题目描述 为了庆祝博格丹的生日，他的母亲送给他一棵有$n$个节点的树，树的第$i$条边上写了一个数字$x_i$。顺带提醒一下，一棵树指的是一个由无向边连接的无环连通图。在礼物被送出之后，有$m$位访客陆续来到博格丹家中参加派对。第$i$位访客会进行如下两种操作其中之一： >1.选择一个数$y_i$和两个节点$a_i$、$b_i$。在这之后，他会沿着树的边走一遍从$a_i$到$b_i$的最短路（当然，在树上这样的路径只有一条）。每当他经过一条边$j$时，他选择的数$y_i$会立刻变成$\lfloor \frac{y_i}{x_j} \rfloor$，也就是$\frac{y_i}{x_i}$向下取整。 > >2.选择第$j$条边$p_j$，把它的边权$x_{p_i}$改成一个正整数$c_i \in [1,x_{p_i}]$。 由于博格丹很替他的客人们着想，他决定简化这个过程。你需要写一个程序处理访客们的操作，并且对于每一个第一种操作$i$，输出$y_i$最后的值。 ## 输入输出格式 ### 输入格式 输入的第一行包含两个整数$n$、$m$（$2\le n\le200000$，$1\le m\le200000$），分别表示树的节点数和访客的数量。 接下来$n-1$行描述每一条边的信息。这些行中的第$i$行包含三个整数$u_i$，$v_i$，$x_i$（$1\le u_i,v_i\le n,u_i\ne v_i,1\le x_i \le 10^{18}$），表示节点$u_i$和$v_i$之间有一条写有$x_i$的无向边。 接下来$m$行描述访客们的操作。每一行包含三个或者四个整数，有如下两种情况： * $1\ a_i\ b_i\ c_i\ $表示操作1 * $2\ p_i\ c_i\ $表示操作2 你可以认为每一个询问都是合法的，也就是说$1\le a_i,b_i\le n$，$1\le p_i\le n-1$，$1\le y_i\le10^{18}$并且$1\le c_i\le x_{p_i}$，此时的$x_{p_i}$不一定和最开始的$x_{p_i}$相等，因为它可能已经被更新过。所有边按照$1\sim n-1$的标号依次在输入中给出。 ### 输出格式 对于每一个询问1，输出一行，从$a_i$走到$b_i$后$y_i$最终的值