Points on Plane

题意翻译

题目描述 给出$N$个整点$(x_i,y_i)$，求一个排列$p_i$，使得$\sum\limits_{i=2}^N |x_{p_i} - x_{p_{i-1}}| + |y_{p_i} - y_{p_{i-1}}| \leq 2.5 \times 10^9$。 输入数据 输入的第一行一个正整数$N(1 \leq N \leq 10^6)$表示点的数量，接下来$N$行每行两个非负整数$x_i,y_i(0 \leq x_i,y_i \leq 10^6)$描述一个点。 输出数据 一行$N$个数表示你给出的排列，每两个数之间用一个空格隔开。

题目描述

On a plane are $ n $ points ( $ x_{i} $ , $ y_{i} $ ) with integer coordinates between $ 0 $ and $ 10^{6} $ . The distance between the two points with numbers $ a $ and $ b $ is said to be the following value: 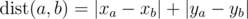 (the distance calculated by such formula is called Manhattan distance). We call a hamiltonian path to be some permutation $ p_{i} $ of numbers from $ 1 $ to $ n $ . We say that the length of this path is value 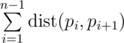. Find some hamiltonian path with a length of no more than $ 25×10^{8} $ . Note that you do not have to minimize the path length.

输入输出格式

输入格式

The first line contains integer $ n $ ( $ 1<=n<=10^{6} $ ). The $ i+1 $ -th line contains the coordinates of the $ i $ -th point: $ x_{i} $ and $ y_{i} $ ( $ 0<=x_{i},y_{i}<=10^{6} $ ). It is guaranteed that no two points coincide.

输出格式

Print the permutation of numbers $ p_{i} $ from $ 1 $ to $ n $ — the sought Hamiltonian path. The permutation must meet the inequality 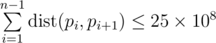. If there are multiple possible answers, print any of them. It is guaranteed that the answer exists.

输入输出样例

输入样例 #1

5
0 7
8 10
3 4
5 0
9 12

输出样例 #1

4 3 1 2 5 

说明

In the sample test the total distance is:  $ (|5-3|+|0-4|)+(|3-0|+|4-7|)+(|0-8|+|7-10|)+(|8-9|+|10-12|)=2+4+3+3+8+3+1+2=26 $