Tavas on the Path

题意翻译

给定一棵 $n$ 个节点的树，每条边有边权。 有 $m$ 个询问，形式为 $(u,v,l)$，求 $u$ 到 $v$ 的路径，假设长度为 $p$，第 $i$ 条边权值为 $x_i$，构造一个长度为 $p$ 的 01串 $s$，如果 $x_i\ge l$，那么 $s_i=1$，否则 $s_i=0$。 对于得到的串 $s$，假设它有 $k$ 段连续的 1，第 $i$ 段长度为 $p_i$，那么要你输出所有 $f_{p_i}$ 的和，其中 $f$ 数组一开始就给出。

题目描述

Tavas lives in Tavaspolis. Tavaspolis has $ n $ cities numbered from $ 1 $ to $ n $ connected by $ n-1 $ bidirectional roads. There exists a path between any two cities. Also each road has a length. Tavas' favorite strings are binary strings (they contain only 0 and 1). For any binary string like $ s=s_{1}s_{2}...\ s_{k} $ , $ T(s) $ is its $ Goodness $ . $ T(s) $ can be calculated as follows: Consider there are exactly $ m $ blocks of $ 1 $ s in this string (a block of $ 1 $ s in $ s $ is a maximal consecutive substring of $ s $ that only contains $ 1 $ ) with lengths $ x_{1},x_{2},...,x_{m} $ . Define 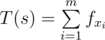 where $ f $ is a given sequence (if $ m=0 $ , then $ T(s)=0 $ ). Tavas loves queries. He asks you to answer $ q $ queries. In each query he gives you numbers $ v,u,l $ and you should print following number: Consider the roads on the path from city $ v $ to city $ u $ : $ e_{1},e_{2},...,e_{x} $ . Build the binary string $ b $ of length $ x $ such that: $ b_{i}=1 $ if and only if $ l<=w(e_{i}) $ where $ w(e) $ is the length of road $ e $ . You should print $ T(b) $ for this query.

输入输出格式

输入格式

The first line of input contains integers $ n $ and $ q $ ( $ 2<=n<=10^{5} $ and $ 1<=q<=10^{5} $ ). The next line contains $ n-1 $ space separated integers $ f_{1},f_{2},...,f_{n-1} $ ( $ |f_{i}|<=1000 $ ). The next $ n-1 $ lines contain the details of the roads. Each line contains integers $ v,u $ and $ w $ and it means that there's a road between cities $ v $ and $ u $ of length $ w $ ( $ 1<=v,u<=n $ and $ 1<=w<=10^{9} $ ). The next $ q $ lines contain the details of the queries. Each line contains integers $ v,u,l $ ( $ 1<=v,u<=n $ , $ v≠u $ and $ 1<=l<=10^{9} $ ).

输出格式

Print the answer of each query in a single line.

输入输出样例

输入样例 #1

2 3
10
1 2 3
1 2 2
1 2 3
1 2 4

输出样例 #1

10
10
0

输入样例 #2

6 6
-5 0 0 2 10
1 2 1
2 3 2
3 4 5
4 5 1
5 6 5
1 6 1
1 6 2
1 6 5
3 6 5
4 6 4
1 4 2

输出样例 #2

10
-5
-10
-10
-5
0