Simplified Nonogram

题意翻译

给出序列 $ a_{1},a_{2},\cdots,a_{n} $，$ b_{1},b_{2},\cdots,b_{m} $，构造一个 $n\times m$ 的 $01$ 矩阵，满足： - 对每个 $1\le i\le n$，第 $i$ 行的极长连续 $1$ 段数量为 $a_i$。 - 对每个 $1\le j\le m$，第 $j$ 列的极长连续 $1$ 段数量为 $b_i$。 输出时对 $0$ 输出 `.`，对 $1$ 输出 `*`。 $1\le n\le 5$，$1\le m\le 20$，保证有解。

题目描述

In this task you have to write a program dealing with nonograms on fields no larger than $ 5×20 $ . Simplified nonogram is a task where you have to build such field (each cell is either white or black) that satisfies the given information about rows and columns. For each row and each column the number of contiguous black segments is specified. For example if size of the field is $ n=3,m=5 $ , аnd numbers of contiguous black segments in rows are: $ [2,3,2] $ and in columns are: $ [1,0,1,2,1] $ then the solution may look like: 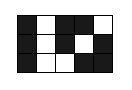It is guaranteed that on each test in the testset there exists at least one solution.

输入输出格式

输入格式

In the first line there follow two integers $ n $ , $ m $ ( $ 1<=n<=5,1<=m<=20 $ ) — number of rows and number of columns respectively. Second line contains $ n $ integers $ a_{1},a_{2},...,a_{n} $ where $ a_{i} $ is the number of contiguous black segments in $ i $ -th row of the field. Similarly, third line contains $ m $ integers $ b_{1},b_{2},...,b_{m} $ where $ b_{i} $ is the number of contiguous black segments in the $ i $ -th column of the field. It is guaranteed that there exists at least one solution.

输出格式

Output any possible solution. Output should consist of $ n $ lines each containing $ m $ characters. Denote white cell as "." and black cell as "\*".

输入输出样例

输入样例 #1

3 5
2 3 2
1 0 1 2 1

输出样例 #1

*.**.
*.*.*
*..**

输入样例 #2

3 3
2 1 2
2 1 2

输出样例 #2

*.*
.*.
*.*

输入样例 #3

3 3
1 0 1
2 2 2

输出样例 #3

***
...
***