Triangles 3000

题意翻译

## 题目描述 给定平面上的$n$个不平行的直线。第$i$条直线以方程$a_ix+b_iy=c_i$的方式给定。没有三线交于一点的情况。 求出任意三条直线形成的三角形的面积之和。 ## 输入格式 第一行一个整数，$n$。 接下来$n$行，每行三个整数，$a_i$，$b_i$，$c_i$。 数据满足$n \leq 3,000$, $-100\leq a_i,b_i\leq 100$, ${a_i}^2+{b_i}^2\geq 0$, $-1000 \leq c_i \leq 10000$ 数据保证没有两条直线平行，任意两条直线的夹角$\geq 10^{-4}$ $I$是直线的交点的集合，即$I=\left\{l_{i} \cap l_{j} | i<j\right\}$。对于$a\in I$，有$a$的座标不超过$10^6$，且对于另一任意点$b$满足$b \in I$，a和b的距离大于等于$10^{-5}$. ## 输出格式 输出答案。允许误差$10^{-4}$。 ## 样例解释 共4个三角形，面积为$0.25$, $0.5$, $2$, $2.25$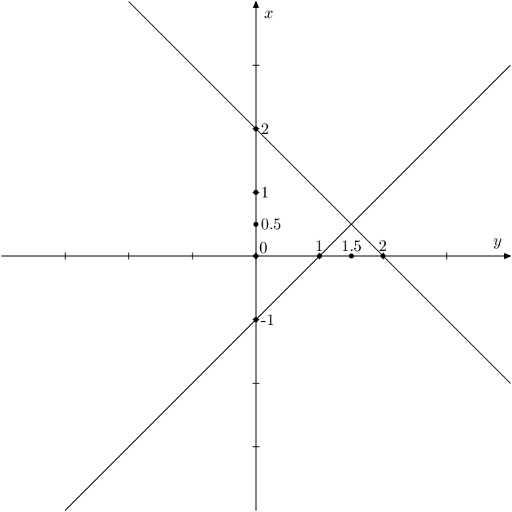 

题目描述

You are given a set $ L={l_{1},l_{2},...,l_{n}} $ of $ n $ pairwise non-parallel lines on the Euclidean plane. The $ i $ -th line is given by an equation in the form of $ a_{i}x+b_{i}y=c_{i} $ . $ L $ doesn't contain three lines coming through the same point. A subset of three distinct lines is chosen equiprobably. Determine the expected value of the area of the triangle formed by the three lines.

输入输出格式

输入格式

The first line of the input contains integer $ n $ ( $ 3<=n<=3000 $ ). Each of the next lines contains three integers $ a_{i},b_{i},c_{i} $ ( $ -100<=a_{i},b_{i}<=100 $ , $ a_{i}^{2}+b_{i}^{2}&gt;0 $ , $ -10000<=c_{i}<=10000 $ ) — the coefficients defining the $ i $ -th line. It is guaranteed that no two lines are parallel. Besides, any two lines intersect at angle at least $ 10^{-4} $ radians. If we assume that $ I $ is a set of points of pairwise intersection of the lines (i. e. ), then for any point  it is true that the coordinates of $ a $ do not exceed $ 10^{6} $ by their absolute values. Also, for any two distinct points  the distance between $ a $ and $ b $ is no less than $ 10^{-5} $ .

输出格式

Print a single real number equal to the sought expected value. Your answer will be checked with the absolute or relative error $ 10^{-4} $ .

输入输出样例

输入样例 #1

4
1 0 0
0 1 0
1 1 2
-1 1 -1

输出样例 #1

1.25

说明

A sample from the statement is shown below. There are four triangles on the plane, their areas are $ 0.25,0.5,2,2.25 $ . 

题意翻译

## 题目描述 给定平面上的$n$个不平行的直线。第$i$条直线以方程$a_ix+b_iy=c_i$的方式给定。没有三线交于一点的情况。 求出任意三条直线形成的三角形的面积之和。 ## 输入格式 第一行一个整数，$n$。 接下来$n$行，每行三个整数，$a_i$，$b_i$，$c_i$。 数据满足$n \leq 3,000$, $-100\leq a_i,b_i\leq 100$, ${a_i}^2+{b_i}^2\geq 0$, $-1000 \leq c_i \leq 10000$ 数据保证没有两条直线平行，任意两条直线的夹角$\geq 10^{-4}$ $I$是直线的交点的集合，即$I=\left\{l_{i} \cap l_{j} | i<j\right\}$。对于$a\in I$，有$a$的座标不超过$10^6$，且对于另一任意点$b$满足$b \in I$，a和b的距离大于等于$10^{-5}$. ## 输出格式 输出答案。允许误差$10^{-4}$。 ## 样例解释 共4个三角形，面积为$0.25$, $0.5$, $2$, $2.25$