Subsequences Return

题意翻译

设 $s_k(x)$ 表示 $x$ 在 $k$ 进制下各位数的和 $\bmod k$ 的值。给出 $k$，现有序列 $[s_k(0),s_k(1),\ldots, s_k(n-1)]$。 求这个序列有多少个本质不同的子序列。 $n\leq 10^{18},k\leq 30$。

题目描述

Assume that $ s_{k}(n) $ equals the sum of digits of number $ n $ in the $ k $ -based notation. For example, $ s_{2}(5)=s_{2}(101_{2})=1+0+1=2 $ , $ s_{3}(14)=s_{3}(112_{3})=1+1+2=4 $ . The sequence of integers $ a_{0},...,a_{n-1} $ is defined as 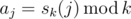. Your task is to calculate the number of distinct subsequences of sequence $ a_{0},...,a_{n-1} $ . Calculate the answer modulo $ 10^{9}+7 $ . Sequence $ a_{1},...,a_{k} $ is called to be a subsequence of sequence $ b_{1},...,b_{l} $ , if there is a sequence of indices $ 1<=i_{1}&lt;...&lt;i_{k}<=l $ , such that $ a_{1}=b_{i1} $ , ..., $ a_{k}=b_{ik} $ . In particular, an empty sequence (i.e. the sequence consisting of zero elements) is a subsequence of any sequence.

输入输出格式

输入格式

The first line contains two space-separated numbers $ n $ and $ k $ ( $ 1<=n<=10^{18} $ , $ 2<=k<=30 $ ).

输出格式

In a single line print the answer to the problem modulo $ 10^{9}+7 $ .

输入输出样例

输入样例 #1

4 2

输出样例 #1

11

输入样例 #2

7 7

输出样例 #2

128

说明

In the first sample the sequence $ a_{i} $ looks as follows: $ (0,1,1,0) $ . All the possible subsequences are: $ (),(0),(0,0),(0,1),(0,1,0),(0,1,1),(0,1,1,0),(1),(1,0),(1,1),(1,1,0). $ In the second sample the sequence $ a_{i} $ looks as follows: $ (0,1,2,3,4,5,6) $ . The subsequences of this sequence are exactly all increasing sequences formed from numbers from 0 to 6. It is easy to see that there are $ 2^{7}=128 $ such sequences.