Hiking

题意翻译

### 题目描述 一个旅行者正在计划沿着河水进行一场水上远足。经过探测，他已经探明了这条河上适合晚上休息的$n$个地点，记录了这些地点与出发点的距离。 上述的每一个地点都有一个美丽度。也就是说，对于第$i$个地点，它和起点的距离为$x_i$，它的美丽度为$b_i$。 上述的每一个地点都在出发点的下游，且这个旅行者在旅行的时候只会顺流而下。 简言之，我们可以把河流看成一个数轴，出发点的坐标是$0$，第$i$个地点的坐标是$x_i$。旅行者只会沿正方向前进。 这个旅行者对他一天的前进距离，设定了一个基准值$l$，如果他某天的所前进的距离大于或小于了这个基准值，都会使他疲劳。假设他一天走了$r_i$的距离，那么他产生的疲劳值为$\sqrt{|r_j-l|}$，他整个旅程的总疲劳值为每一天的疲劳值之和。 显然，这个旅行者晚上需要休息，所以必须到达一个休息地点才能结束一天的行程，并在这个地点过夜。类似于上面的定义，假设他当天晚上在第$i$个地点休息，那么他当天的舒适度为这个地点的美丽度，即$b_i$。他整个旅程的总舒适度是每一天（包括最后一天）的舒适度之和。 现在他希望你帮助他规划旅游路线，确定出每一天在哪个地点休息，他对旅游的天数没有要求，但是要求最后一天必须在第$n$个地点休息。他希望你的这个规划足够合理，使得这次旅行的**总疲劳值除以总舒适度**的结果最小化。 ### 输入格式 第一行，两个整数，$n$，$l$，分别表示休息地点的个数和每日旅行距离的基准值。 接下来$n$行，每行两个整数，$x_i,b_i$，保证$x_i$严格递增。 ### 输出格式 按顺序输出你所规划的每一天的休息地点的序号，用空格隔开，必须以$n$号地点结束。 ### 数据范围 $1\leq n \leq 1000$ $1\leq l \leq 10^5$ $1\leq x_i,b_i \leq10^6$ ### 样例解释 样例中总疲劳值除以总舒适度的最小值约为$0.097549$，即$(\frac{1+1+\sqrt 2 +0}{10+ 10+ 5+ 10})$

题目描述

A traveler is planning a water hike along the river. He noted the suitable rest points for the night and wrote out their distances from the starting point. Each of these locations is further characterized by its picturesqueness, so for the $ i $ -th rest point the distance from the start equals $ x_{i} $ , and its picturesqueness equals $ b_{i} $ . The traveler will move down the river in one direction, we can assume that he will start from point $ 0 $ on the coordinate axis and rest points are points with coordinates $ x_{i} $ . Every day the traveler wants to cover the distance $ l $ . In practice, it turns out that this is not always possible, because he needs to end each day at one of the resting points. In addition, the traveler is choosing between two desires: cover distance $ l $ every day and visit the most picturesque places. Let's assume that if the traveler covers distance $ r_{j} $ in a day, then he feels frustration 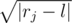, and his total frustration over the hike is calculated as the total frustration on all days. Help him plan the route so as to minimize the relative total frustration: the total frustration divided by the total picturesqueness of all the rest points he used. The traveler's path must end in the farthest rest point.

输入输出格式

输入格式

A traveler is planning a water hike along the river. He noted the suitable rest points for the night and wrote out their distances from the starting point. Each of these locations is further characterized by its picturesqueness, so for the $ i $ -th rest point the distance from the start equals $ x_{i} $ , and its picturesqueness equals $ b_{i} $ . The traveler will move down the river in one direction, we can assume that he will start from point $ 0 $ on the coordinate axis and rest points are points with coordinates $ x_{i} $ . Every day the traveler wants to cover the distance $ l $ . In practice, it turns out that this is not always possible, because he needs to end each day at one of the resting points. In addition, the traveler is choosing between two desires: cover distance $ l $ every day and visit the most picturesque places. Let's assume that if the traveler covers distance $ r_{j} $ in a day, then he feels frustration 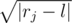, and his total frustration over the hike is calculated as the total frustration on all days. Help him plan the route so as to minimize the relative total frustration: the total frustration divided by the total picturesqueness of all the rest points he used. The traveler's path must end in the farthest rest point.

输出格式

A traveler is planning a water hike along the river. He noted the suitable rest points for the night and wrote out their distances from the starting point. Each of these locations is further characterized by its picturesqueness, so for the $ i $ -th rest point the distance from the start equals $ x_{i} $ , and its picturesqueness equals $ b_{i} $ . The traveler will move down the river in one direction, we can assume that he will start from point $ 0 $ on the coordinate axis and rest points are points with coordinates $ x_{i} $ . Every day the traveler wants to cover the distance $ l $ . In practice, it turns out that this is not always possible, because he needs to end each day at one of the resting points. In addition, the traveler is choosing between two desires: cover distance $ l $ every day and visit the most picturesque places. Let's assume that if the traveler covers distance $ r_{j} $ in a day, then he feels frustration 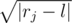, and his total frustration over the hike is calculated as the total frustration on all days. Help him plan the route so as to minimize the relative total frustration: the total frustration divided by the total picturesqueness of all the rest points he used. The traveler's path must end in the farthest rest point.

输入输出样例

输入样例 #1

5 9
10 10
20 10
30 1
31 5
40 10

输出样例 #1

1 2 4 5 

说明

In the sample test the minimum value of relative total frustration approximately equals 0.097549. This value can be calculated as .