Valid Sets

题意翻译

给定 $n$ 个点的树，点有点权，求满足最大点权与最小点权之差小于等于 $d$ 的连通子图数目。答案对 $10^9 + 7$ 取模。

题目描述

As you know, an undirected connected graph with $ n $ nodes and $ n-1 $ edges is called a tree. You are given an integer $ d $ and a tree consisting of $ n $ nodes. Each node $ i $ has a value $ a_{i} $ associated with it. We call a set $ S $ of tree nodes valid if following conditions are satisfied: 1. $ S $ is non-empty. 2. $ S $ is connected. In other words, if nodes $ u $ and $ v $ are in $ S $ , then all nodes lying on the simple path between $ u $ and $ v $ should also be presented in $ S $ . 3. 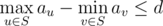. Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo $ 1000000007 $ ( $ 10^{9}+7 $ ).

输入输出格式

输入格式

The first line contains two space-separated integers $d$ ($0 \le d \le 2000$) and $n$ ($1 \le n \le 2000$). The second line contains $n$ space-separated positive integers $a_1, a_2, \ldots, a_n$ ($1 \le a_i \le 2000$). Then the next $n - 1$ line each contain pair of integers $u$ and $v$ ($1 \le u, v \le n$) denoting that there is an edge between $u$ and $v$. It is guaranteed that these edges form a tree.

输出格式

Print the number of valid sets modulo $ 1000000007 $ .

输入输出样例

输入样例 #1

1 4
2 1 3 2
1 2
1 3
3 4

输出样例 #1

8

输入样例 #2

0 3
1 2 3
1 2
2 3

输出样例 #2

3

输入样例 #3

4 8
7 8 7 5 4 6 4 10
1 6
1 2
5 8
1 3
3 5
6 7
3 4

输出样例 #3

41

说明

In the first sample, there are exactly 8 valid sets: $ {1},{2},{3},{4},{1,2},{1,3},{3,4} $ and $ {1,3,4} $ . Set $ {1,2,3,4} $ is not valid, because the third condition isn't satisfied. Set $ {1,4} $ satisfies the third condition, but conflicts with the second condition.