Dreamoon and Sums

题意翻译

给定$a,b(a,b\le10^7)$，求 $$\sum_x x\times [1\le\frac{\lfloor x/b\rfloor}{x\mod b}\le a]$$ 上式的中括号为艾佛森括号。 答案对$10^9+7$取模。

题目描述

Dreamoon loves summing up something for no reason. One day he obtains two integers $ a $ and $ b $ occasionally. He wants to calculate the sum of all nice integers. Positive integer $ x $ is called nice if 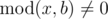 and 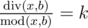, where $ k $ is some integer number in range $ \[1,a\] $ . By 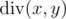 we denote the quotient of integer division of $ x $ and $ y $ . By 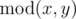 we denote the remainder of integer division of $ x $ and $ y $ . You can read more about these operations here: http://goo.gl/AcsXhT. The answer may be large, so please print its remainder modulo $ 1000000007 $ ( $ 10^{9}+7 $ ). Can you compute it faster than Dreamoon?

输入输出格式

输入格式

The single line of the input contains two integers $ a $ , $ b $ ( $ 1<=a,b<=10^{7} $ ).

输出格式

Print a single integer representing the answer modulo $ 1000000007 $ ( $ 10^{9}+7 $ ).

输入输出样例

输入样例 #1

1 1

输出样例 #1

0

输入样例 #2

2 2

输出样例 #2

8

说明

For the first sample, there are no nice integers because  is always zero. For the second sample, the set of nice integers is $ {3,5} $ .