Prime Number

题意翻译

Simon 有一个质数 $x$ 和若干非负整数 $a_1,a_2,\dots,a_n$. Simon 很喜欢分数。今天，他在纸上写出了一个数 $\dfrac{1}{x^{a_1}}+\dfrac{1}{x^{a_2}}+\cdots+\dfrac{1}{x^{a_n}}$。Simon 通分并计算出这个和式之后得到了一个分数 $\dfrac st$，其中 $t=x^{a_1+a_2+\dots+a_n}$。现在，Simon 希望化简这个结果。 请帮助 Simon 求出 $s$ 和 $t$ 的最大公因数。因为这个最大公因数可能很大，输出它除 $1000000007$（$10^9+7$）的余数。 输入第一行包括两个正整数 $n$ 和 $x$（$1\le n\le10^5$，$2\le x\le10^9$）——数组的大小和这个质数，第二行包括 $n$ 个用空格隔开的整数 $a_1,a_2,\dots,a_n$（$0\le a_1\le a_2\le\dots\le a_n\le10^9$）. 输出一个整数——问题的答案除 $1000000007$（$10^9+7$）的余数。

题目描述

Simon has a prime number $ x $ and an array of non-negative integers $ a_{1},a_{2},...,a_{n} $ . Simon loves fractions very much. Today he wrote out number 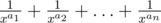 on a piece of paper. After Simon led all fractions to a common denominator and summed them up, he got a fraction: , where number $ t $ equals $ x^{a_{1}+a_{2}+...+a_{n}} $ . Now Simon wants to reduce the resulting fraction. Help him, find the greatest common divisor of numbers $ s $ and $ t $ . As GCD can be rather large, print it as a remainder after dividing it by number $ 1000000007 $ ( $ 10^{9}+7 $ ).

输入输出格式

输入格式

The first line contains two positive integers $ n $ and $ x $ ( $ 1<=n<=10^{5} $ , $ 2<=x<=10^{9} $ ) — the size of the array and the prime number. The second line contains $ n $ space-separated integers $ a_{1},a_{2},...,a_{n} $ ( $ 0<=a_{1}<=a_{2}<=...<=a_{n}<=10^{9} $ ).

输出格式

Print a single number — the answer to the problem modulo $ 1000000007 $ ( $ 10^{9}+7 $ ).

输入输出样例

输入样例 #1

2 2
2 2

输出样例 #1

8

输入样例 #2

3 3
1 2 3

输出样例 #2

27

输入样例 #3

2 2
29 29

输出样例 #3

73741817

输入样例 #4

4 5
0 0 0 0

输出样例 #4

1

说明

In the first sample . Thus, the answer to the problem is $ 8 $ . In the second sample, . The answer to the problem is $ 27 $ , as $ 351=13·27 $ , $ 729=27·27 $ . In the third sample the answer to the problem is $ 1073741824 mod 1000000007=73741817 $ . In the fourth sample . Thus, the answer to the problem is $ 1 $ .