Find Maximum

题意翻译

### 题目描述 Valera 有一个 $n$ 个数的 **非负整数** 数组 $a$ ，其元素分别为 $a_0,a_1,\cdots,a_{n-1}$。同时有一个函数 $f(x)=\sum_{i=0}^{n-1}a_i\cdot bit(i)$，$bit(i)$ 指的是数字 $x$ 在二进制中第 $i$ 位的值是否为 1。 举个例子，当 $n=4,x=11(11=2^0+2^1+2^3)$ 时，$f(x)=a_0+a_1+a_3$。 对于所有 $0\le x \le m$ 的整数 $x$ ，请求出 $f(x)$ 的最大值。 ### 输入格式 第一行，输入 $n$ 。 接下来一行，输入数组 $a$ 。 最后一行输入一个由 $n$ 个数组成的数字序列 $s$ ，$s$ 即为 $m$ 的二进制翻转后的数字序列。（ 也就是 $m=\sum_{i=0}^{n-1}2^i\cdot s_i$ ）数字与数字之间没有空格。 ### 输出格式 一行一个整数，表示 $f(x)$ 的最大值。 ### 数据范围 - $1 \le n \le 10^5$ - $0 \le a_i \le 10^4$ - $0\le s_i \le 1$

题目描述

Valera has array $ a $ , consisting of $ n $ integers $ a_{0},a_{1},...,a_{n-1} $ , and function $ f(x) $ , taking an integer from $ 0 $ to $ 2^{n}-1 $ as its single argument. Value $ f(x) $ is calculated by formula 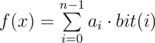, where value $ bit(i) $ equals one if the binary representation of number $ x $ contains a $ 1 $ on the $ i $ -th position, and zero otherwise. For example, if $ n=4 $ and $ x=11 $ $ (11=2^{0}+2^{1}+2^{3}) $ , then $ f(x)=a_{0}+a_{1}+a_{3} $ . Help Valera find the maximum of function $ f(x) $ among all $ x $ , for which an inequality holds: $ 0<=x<=m $ .

输入输出格式

输入格式

The first line contains integer $ n $ $ (1<=n<=10^{5}) $ — the number of array elements. The next line contains $ n $ space-separated integers $ a_{0},a_{1},...,a_{n-1} $ $ (0<=a_{i}<=10^{4}) $ — elements of array $ a $ . The third line contains a sequence of digits zero and one without spaces $ s_{0}s_{1}...\ s_{n-1} $ — the binary representation of number $ m $ . Number $ m $ equals .

输出格式

Print a single integer — the maximum value of function $ f(x) $ for all .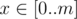

输入输出样例

输入样例 #1

2
3 8
10

输出样例 #1

3

输入样例 #2

5
17 0 10 2 1
11010

输出样例 #2

27

说明

In the first test case $ m=2^{0}=1,f(0)=0,f(1)=a_{0}=3 $ . In the second sample $ m=2^{0}+2^{1}+2^{3}=11 $ , the maximum value of function equals $ f(5)=a_{0}+a_{2}=17+10=27 $ .

题意翻译

### 题目描述 Valera 有一个 $n$ 个数的 **非负整数** 数组 $a$ ，其元素分别为 $a_0,a_1,\cdots,a_{n-1}$。同时有一个函数 $f(x)=\sum_{i=0}^{n-1}a_i\cdot bit(i)$，$bit(i)$ 指的是数字 $x$ 在二进制中第 $i$ 位的值是否为 1。 举个例子，当 $n=4,x=11(11=2^0+2^1+2^3)$ 时，$f(x)=a_0+a_1+a_3$。 对于所有 $0\le x \le m$ 的整数 $x$ ，请求出 $f(x)$ 的最大值。 ### 输入格式 第一行，输入 $n$ 。 接下来一行，输入数组 $a$ 。 最后一行输入一个由 $n$ 个数组成的数字序列 $s$ ，$s$ 即为 $m$ 的二进制翻转后的数字序列。（ 也就是 $m=\sum_{i=0}^{n-1}2^i\cdot s_i$ ）数字与数字之间没有空格。 ### 输出格式 一行一个整数，表示 $f(x)$ 的最大值。 ### 数据范围 - $1 \le n \le 10^5$ - $0 \le a_i \le 10^4$ - $0\le s_i \le 1$