301741: CF330B. Road Construction
Memory Limit:256 MB
Time Limit:2 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Road Construction
题意翻译
n座城市,编号1-n,1号为首都,原计划修m条道路,现在要削减成本,取消一些道路,使得成本最小。要求,每个城市都能通往首都,原计划每座城市到首都的最短距离在新计划里面还是不变。问在保证源点1 到其他各点的距离最短的情况下,最少的 花费是多少?题目描述
A country has $ n $ cities. Initially, there is no road in the country. One day, the king decides to construct some roads connecting pairs of cities. Roads can be traversed either way. He wants those roads to be constructed in such a way that it is possible to go from each city to any other city by traversing at most two roads. You are also given $ m $ pairs of cities — roads cannot be constructed between these pairs of cities. Your task is to construct the minimum number of roads that still satisfy the above conditions. The constraints will guarantee that this is always possible.输入输出格式
输入格式
The first line consists of two integers $ n $ and $ m $ 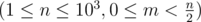. Then $ m $ lines follow, each consisting of two integers $ a_{i} $ and $ b_{i} $ ( $ 1<=a_{i},b_{i}<=n $ , $ a_{i}≠b_{i} $ ), which means that it is not possible to construct a road connecting cities $ a_{i} $ and $ b_{i} $ . Consider the cities are numbered from 1 to $ n $ . It is guaranteed that every pair of cities will appear at most once in the input.
输出格式
You should print an integer $ s $ : the minimum number of roads that should be constructed, in the first line. Then $ s $ lines should follow, each consisting of two integers $ a_{i} $ and $ b_{i} $ ( $ 1<=a_{i},b_{i}<=n,a_{i}≠b_{i} $ ), which means that a road should be constructed between cities $ a_{i} $ and $ b_{i} $ . If there are several solutions, you may print any of them.
输入输出样例
输入样例 #1
4 1
1 3
输出样例 #1
3
1 2
4 2
2 3