Maximum Waterfall

题意翻译

Emuskald想设计一座人工瀑布。 现代的人工瀑布由多个水平面板组成，这些面板固定在宽阔的平墙上。 水沿着墙的顶部从一个板流向另一个板，直到到达墙的底部。 墙壁上有高度t和n个面板。每个板都是高度为h[i]的水平段 墙的高度为t，墙上有n个板。每个板在高度h[i]处为水平段 从l[i]开始，到r[i]结束。第i个面板连接平面的点（l[i]，r[i]）。 墙顶可视为连接点（-10^9，t）的板。 同样，墙的底部可以被视为连接点（-10^9,0）和（10^9,0）的板。 没有两个面板重叠。 Emuskald知道，为了使瀑布美观，只有在满足以下条件的情况下，它才能从面板i流向面板j 1.最大值（l[i]，l[j]）；min（r[i]，r[j]）（面板重叠的水平投影）; 2. 对于 h[j]和h[i],满足板j在板i之下; 3.前两个条件不适用于对（i，k）和（k，j）的板k（h[j]，h[k]，h[i]）。 那么的流量等于min（r[i]，r[j]）-max（l[i]，l[j]）瀑布的重叠部分。 Emuskald已经决定，在他的瀑布中，水将以一条从上到下的单一路径流动。 如果水流到面板（墙底部除外），水将进一步下落到正下方的一个面板。 然后将瀑布中的总水量定义为瀑布路径上两个连续面板之间的最小重叠。 注意： 瀑布由面板顶部->p1->p2…->的单一路径组成底部 瀑布流是路径顶部->p1->p2…->底部 为了建造一个真正伟大的瀑布，Emuskald必须最大限度地利用水流，但是有太多的板，他很难规划他的创作。 下面是Emuskald想要的瀑布示例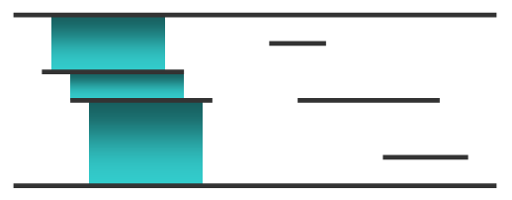：  请帮助Emuskald找到最大可能水流的价值。

题目描述

Emuskald was hired to design an artificial waterfall according to the latest trends in landscape architecture. A modern artificial waterfall consists of multiple horizontal panels affixed to a wide flat wall. The water flows down the top of the wall from panel to panel until it reaches the bottom of the wall. The wall has height $ t $ and has $ n $ panels on the wall. Each panel is a horizontal segment at height $ h_{i} $ which begins at $ l_{i} $ and ends at $ r_{i} $ . The $ i $ -th panel connects the points $ (l_{i},h_{i}) $ and $ (r_{i},h_{i}) $ of the plane. The top of the wall can be considered a panel connecting the points $ (-10^{9},t) $ and $ (10^{9},t) $ . Similarly, the bottom of the wall can be considered a panel connecting the points $ (-10^{9},0) $ and $ (10^{9},0) $ . No two panels share a common point. Emuskald knows that for the waterfall to be aesthetically pleasing, it can flow from panel $ i $ to panel $ j $ () only if the following conditions hold: 1. $ max(l_{i},l_{j})<min(r_{i},r_{j}) $ (horizontal projections of the panels overlap); 2. $ h_{j}<h_{i} $ (panel $ j $ is below panel $ i $ ); 3. there is no such panel $ k $ $ (h_{j}<h_{k}<h_{i}) $ that the first two conditions hold for the pairs $ (i,k) $ and $ (k,j) $ . Then the flow for  is equal to $ min(r_{i},r_{j})-max(l_{i},l_{j}) $ , the length of their horizontal projection overlap. Emuskald has decided that in his waterfall the water will flow in a single path from top to bottom. If water flows to a panel (except the bottom of the wall), the water will fall further to exactly one lower panel. The total amount of water flow in the waterfall is then defined as the minimum horizontal projection overlap between two consecutive panels in the path of the waterfall. Formally: 1. the waterfall consists of a single path of panels ; 2. the flow of the waterfall is the minimum flow in the path . To make a truly great waterfall Emuskald must maximize this water flow, but there are too many panels and he is having a hard time planning his creation. Below is an example of a waterfall Emuskald wants: 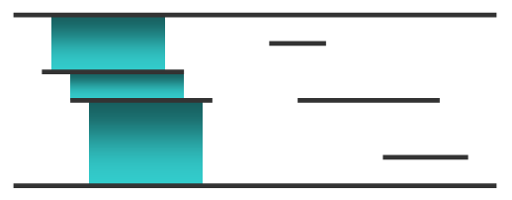Help Emuskald maintain his reputation and find the value of the maximum possible water flow.

输入输出格式

输入格式

The first line of input contains two space-separated integers $ n $ and $ t $ ( $ 1<=n<=10^{5} $ , $ 2<=t<=10^{9} $ ), the number of the panels excluding the top and the bottom panels, and the height of the wall. Each of the $ n $ following lines contain three space-separated integers $ h_{i} $ , $ l_{i} $ and $ r_{i} $ ( $ 0&lt;h_{i}&lt;t $ , $ -10^{9}<=l_{i}&lt;r_{i}<=10^{9} $ ), the height, left and right ends of the $ i $ -th panel segment. It is guaranteed that no two segments share a common point.

输出格式

Output a single integer — the maximum possible amount of water flow in the desired waterfall.

输入输出样例

输入样例 #1

5 6
4 1 6
3 2 7
5 9 11
3 10 15
1 13 16

输出样例 #1

4

输入样例 #2

6 5
4 2 8
3 1 2
2 2 3
2 6 12
1 0 7
1 8 11

输出样例 #2

2

说明

The first test case corresponds to the picture.