Save the City!

题意翻译

#### 题目描述 在 `Aalam-Aara`（意为大地之光）镇，以前没有犯罪，没有罪犯。但随着时间的推移，罪恶开始蔓延到曾经正义的人们的心中。为了解决这个问题，一些长老发现，只要将人口中腐败的部分远离未腐败的部分，犯罪就可以停止。所以，他们正试图建立一个可以关押腐败人民的大院。为确保不法分子逃出大院，需要设置瞭望塔，以便对其进行监视。 由于 `Aalam-Aara` 的人民不是很富有，他们遇到了一个来自某个富裕城镇的商人，他同意将一块地块卖给他们，该地块已经有一条直线围栏 $AB$，沿围栏设置了几个点。可以建瞭望塔。你的任务是帮助他们找出栅栏上可以架设塔楼的点数，以便从那里监视所有罪犯。只能设置一个瞭望塔。如果从瞭望塔到罪犯的视线没有在他和塔之间的任何点穿过情节边缘，即如下图 $1$ 所示，点 $X$、$Y$、$C$ 和 $A$ 是可以从瞭望塔观察到的从 $B$ 点可见，但 $E$ 和 $D$ 点不可见。 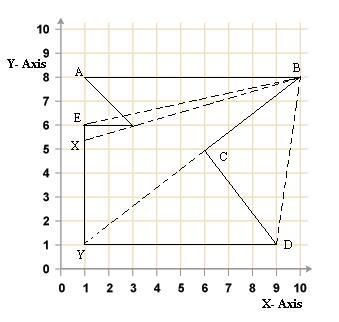\ 　　　　　　　　　　　图$1$ 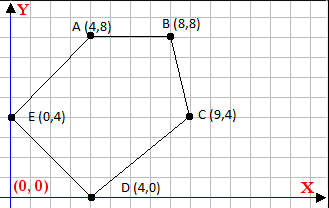\ 　　　　　　　　　　　图$2$ 假设地块为多边形，坐标轴设置为围栏$AB$平行于$x$轴，可以设置瞭望塔的点是直线上的整数点。 例如，在给定的图 $2$ 中，瞭望塔可以设置在 $AB$ 上的五个整数点中的任何一个，即 $(4,8)$、$(5,8)$、$(6,8)$、$(7,8)$ 或 $(8,8)$. 您可以假设没有三个连续的点共线，并且除 $A$ 和 $B$ 之外的所有角点都位于围栏 $AB$ 的同一侧。 给定的多边形不包含自相交。 #### 输入格式 测试用例的第一行将包含顶点数 $n$ $(3 \le n \le 100)$。 接下来的 $n$ 行将包含按多边形顺时针顺序排列的顶点坐标。第 $i$ 行是整数 $x_i$ 和 $y_i$ $(0 \le x_i, y_i \le 10^6)$。 围栏$AB$的端点是前两个点 $(x_1,y_1)$ 和 $(x_2,y_2)$。 #### 输出格式 输出可以设置瞭望塔的点数个数。 #### 提示/说明 图 $2$ 显示了第一个测试用例。 图中的所有点都可以从围栏 $AB$ 上的任何点看到。 因为， $AB$ 有 $5$ 个整数坐标，所以答案是 $5$ 。 对于情况二，围栏 $CD$ 和 $DE$ 不完全可见，因此答案为 $0$ 。

题目描述

In the town of Aalam-Aara (meaning the Light of the Earth), previously there was no crime, no criminals but as the time progressed, sins started creeping into the hearts of once righteous people. Seeking solution to the problem, some of the elders found that as long as the corrupted part of population was kept away from the uncorrupted part, the crimes could be stopped. So, they are trying to set up a compound where they can keep the corrupted people. To ensure that the criminals don't escape the compound, a watchtower needs to be set up, so that they can be watched. Since the people of Aalam-Aara aren't very rich, they met up with a merchant from some rich town who agreed to sell them a land-plot which has already a straight line fence $ AB $ along which a few points are set up where they can put up a watchtower. Your task is to help them find out the number of points on that fence where the tower can be put up, so that all the criminals can be watched from there. Only one watchtower can be set up. A criminal is watchable from the watchtower if the line of visibility from the watchtower to him doesn't cross the plot-edges at any point between him and the tower i.e. as shown in figure 1 below, points $ X $ , $ Y $ , $ C $ and $ A $ are visible from point $ B $ but the points $ E $ and $ D $ are not.  Figure 1  Figure 2 Assume that the land plot is in the shape of a polygon and coordinate axes have been setup such that the fence $ AB $ is parallel to $ x $ -axis and the points where the watchtower can be set up are the integer points on the line. For example, in given figure 2, watchtower can be setup on any of five integer points on $ AB $ i.e. $ (4,8) $ , $ (5,8) $ , $ (6,8) $ , $ (7,8) $ or $ (8,8) $ . You can assume that no three consecutive points are collinear and all the corner points other than $ A $ and $ B $ , lie towards same side of fence $ AB $ . The given polygon doesn't contain self-intersections.

输入输出格式

输入格式

The first line of the test case will consist of the number of vertices $ n $ ( $ 3<=n<=1000 $ ). Next $ n $ lines will contain the coordinates of the vertices in the clockwise order of the polygon. On the $ i $ -th line are integers $ x_{i} $ and $ y_{i} $ ( $ 0<=x_{i},y_{i}<=10^{6} $ ) separated by a space. The endpoints of the fence $ AB $ are the first two points, $ (x_{1},y_{1}) $ and $ (x_{2},y_{2}) $ .

输出格式

Output consists of a single line containing the number of points where the watchtower can be set up.

输入输出样例

输入样例 #1

5
4 8
8 8
9 4
4 0
0 4

输出样例 #1

5

输入样例 #2

5
4 8
5 8
5 4
7 4
2 2

输出样例 #2

0

说明

Figure 2 shows the first test case. All the points in the figure are watchable from any point on fence $ AB $ . Since, $ AB $ has $ 5 $ integer coordinates, so answer is $ 5 $ . For case two, fence $ CD $ and $ DE $ are not completely visible, thus answer is $ 0 $ .