103172: [Atcoder]ABC317 C - Remembering the Days
Description
Score : $300$ points
Problem Statement
A region has $N$ towns numbered $1$ to $N$, and $M$ roads numbered $1$ to $M$.
The $i$-th road connects town $A_i$ and town $B_i$ bidirectionally with length $C_i$.
Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.
Constraints
- $2 \leq N \leq 10$
- $1 \leq M \leq \frac{N(N-1)}{2}$
- $1 \leq A_i < B_i \leq N$
- The pairs $(A_i,B_i)$ are distinct.
- $1\leq C_i \leq 10^8$
- All input values are integers.
Input
The input is given from Standard Input in the following format:
$N$ $M$ $A_1$ $B_1$ $C_1$ $\vdots$ $A_M$ $B_M$ $C_M$
Output
Print the answer.
Sample Input 1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
Sample Output 1
1110
If you travel as $4\to 1\to 3\to 2$, the total length of the roads you traverse is $1110$.
Sample Input 2
10 1 5 9 1
Sample Output 2
1
There may be a town that is not connected to a road.
Sample Input 3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
Sample Output 3
20
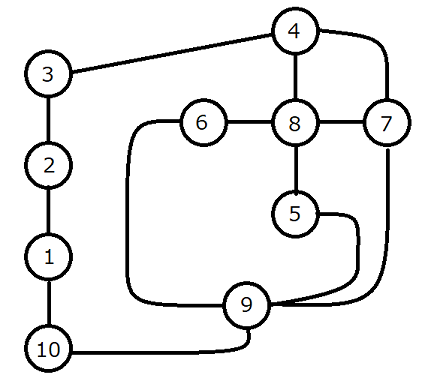
Output
问题描述
有一个包含从1到$N$编号的$N$个城镇的地区,以及从1到$M$编号的$M$条道路。
第$i$条道路双向连接城镇$A_i$和城镇$B_i$,长度为$C_i$。
从任意一个城镇出发,前往另一个城镇,不通过同一个城镇超过一次,找到可能的最大道路总长度。
约束
- $2 \leq N \leq 10$
- $1 \leq M \leq \frac{N(N-1)}{2}$
- $1 \leq A_i < B_i \leq N$
- $(A_i,B_i)$对是唯一的。
- $1\leq C_i \leq 10^8$
- 所有输入值都是整数。
输入
输入将从标准输入中以以下格式给出:
$N$ $M$ $A_1$ $B_1$ $C_1$ $\vdots$ $A_M$ $B_M$ $C_M$
输出
打印答案。
样例输入1
4 4 1 2 1 2 3 10 1 3 100 1 4 1000
样例输出1
1110
如果你走$4\to 1\to 3\to 2$,你经过的道路总长度为$1110$。
样例输入2
10 1 5 9 1
样例输出2
1
可能存在一个不与道路相连的城镇。
样例输入3
10 13 1 2 1 1 10 1 2 3 1 3 4 4 4 7 2 4 8 1 5 8 1 5 9 3 6 8 1 6 9 5 7 8 1 7 9 4 9 10 3
样例输出3
20
