101133: [AtCoder]ABC113 D - Number of Amidakuji
Description
Score: $400$ points
Problem Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw $W$ parallel vertical lines, and then draw horizontal lines that connect them. The length of each vertical line is $H+1$ [cm], and the endpoints of the horizontal lines must be at $1, 2, 3, ...,$ or $H$ [cm] from the top of a vertical line.
A valid amidakuji is an amidakuji that satisfies the following conditions:
- No two horizontal lines share an endpoint.
- The two endpoints of each horizontal lines must be at the same height.
- A horizontal line must connect adjacent vertical lines.
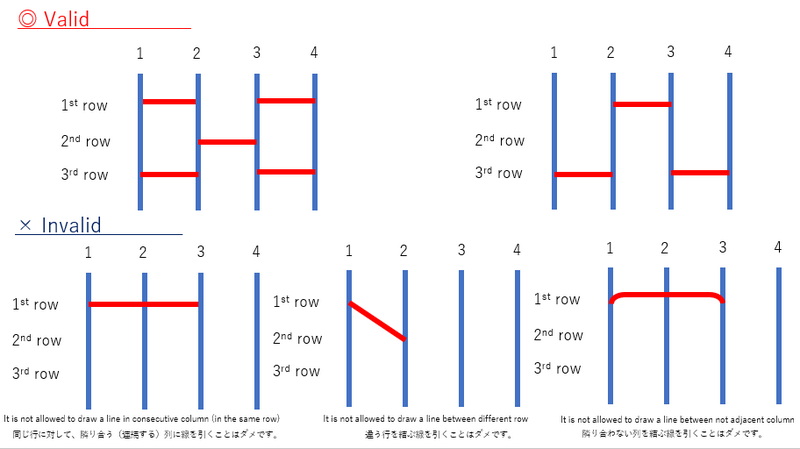
Find the number of the valid amidakuji that satisfy the following condition, modulo $1\ 000\ 000\ 007$: if we trace the path from the top of the leftmost vertical line to the bottom, always following horizontal lines when we encounter them, we reach the bottom of the $K$-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the fourth vertical line from the left.

Constraints
- $H$ is an integer between $1$ and $100$ (inclusive).
- $W$ is an integer between $1$ and $8$ (inclusive).
- $K$ is an integer between $1$ and $W$ (inclusive).
Input
Input is given from Standard Input in the following format:
$H$ $W$ $K$
Output
Print the number of the amidakuji that satisfy the condition, modulo $1\ 000\ 000\ 007$.
Sample Input 1
1 3 2
Sample Output 1
1
Only the following one amidakuji satisfies the condition:

Sample Input 2
1 3 1
Sample Output 2
2
Only the following two amidakuji satisfy the condition:

Sample Input 3
2 3 3
Sample Output 3
1
Only the following one amidakuji satisfies the condition:

Sample Input 4
2 3 1
Sample Output 4
5
Only the following five amidakuji satisfy the condition:

Sample Input 5
7 1 1
Sample Output 5
1
As there is only one vertical line, we cannot draw any horizontal lines. Thus, there is only one amidakuji that satisfies the condition: the amidakuji with no horizontal lines.
Sample Input 6
15 8 5
Sample Output 6
437760187
Be sure to print the answer modulo $1\ 000\ 000\ 007$.